Blog

Ch 2 - Data Science: Statistics vs. Machine Learning

Security Analytics

Authors: Securonix Labs

Introduction

Data science is a field that cuts across several technical disciplines including computer science, statistics, and applied mathematics. The goal of data science is to use scientific methods to extract valuable information from data.

Advances in large-scale data storage and distributed computing have enabled us to deal with the notoriously large volumes of data generated by network and Internet activity. Availability and affordability of high performance computing resources has allowed data scientists to develop sophisticated models and analyze large datasets that were once overwhelming.

Statistics and machine learning are two of the key techniques employed by data science, and they share the same objective: to learn from data. While the differences between them are becoming less pronounced due to the heavy borrowing from each other, it’s important to understand the methods used and the applicability of each to appreciate the whole range of capabilities they bring to data science.

Statistics

Statistics is concerned with making inferences from data. This often involves attempting to understand the underlying mechanism by which data is created and applying an appropriate technique to model the process. In order to do so, assumptions are made about the data to build a tractable model and derive insights.

When the task involves understanding the structure within data to obtain results, statistical models generally excel at identifying the underlying patterns and account for their uncertainty through their probabilistic framework. This usually requires a small number of features and a large quantity of data to ensure that the required estimates are robust in order to derive useful information from the model.

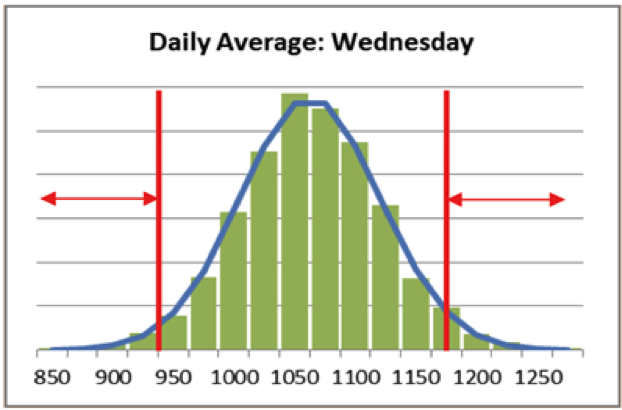
For example, when analyzing daily amounts of transactions, security analysts may be interested in identifying abnormal values for specific days that might indicate malicious activity. They can use statistical reasoning to look at the daily average of transaction amounts and invoke the central limit theorem to justify the assumption that the averages are normally distributed.

Once a normal distribution is fit to the data, its estimated parameters (mean and variance) can be used to define a range of values that are considered normal activity. Those amounts which are outside this range are deemed suspicious as they are improbable and are investigated further by the security analysts.

The blue line is the fitted normal distribution. The anomalous values fall in the range shown by the arrows; these are flagged when observed and sent to the analyst for further inspection.

The detection of anomalous events extends beyond numeric information like daily average transactions. In particular, to estimate and score rare events for non-numeric or categorical data, we need to either understand the underlying data generation process to model it correctly, or to employ additional statistical methods to quantify and scale categorical variables.

In the example below, Multiple Correspondence Analysis (MCA) is used to transform categorical variables into coordinates in the space defined by the major principal components (only two dimensions are shown). The clustering analysis is performed next in the same space to group individuals with similar categories and to identify outliers.

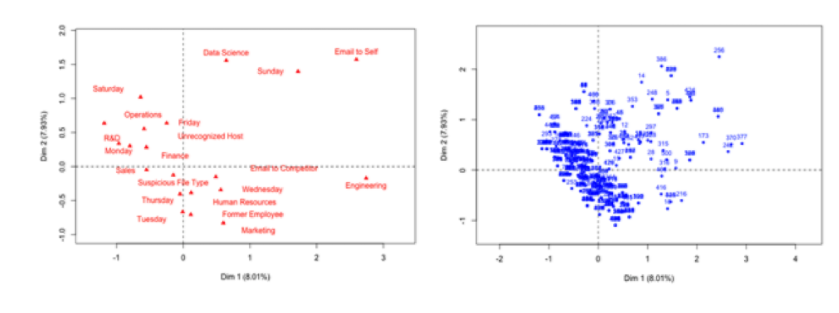
Projection of categories (left) and individuals (right) on the two main principal components of the Multiple Correspondence Analysis (MCA).

Statistics aims to infer the relationships between inputs and outputs and succeeds in explaining the underlying process when all the assumptions on randomization and probability distribution are met. However, many real-life processes, while complex, are far from random, and setting up an experiment to randomize the sample is often not feasible. The statistical model, in this case, might still have high explanatory power, but low predictive power, since it follows invalid assumptions, and therefore might be misleading.

Modern datasets are rich, diverse and high-dimensional, with data aggregated from multiple sources, each representing a complex process on its own. Fitting the right distribution here requires estimating a large number of parameters, and there is a risk of making dubious conclusions by overlooking valuable information, when important characteristics of data go unrecognized, or by capturing wrong information. Inferences are also difficult in cases where the number of features significantly exceeds the number of observations. An accurate statistical model for such problems might be too cumbersome to build, and frequent or even near-real-time updates required to reflect the changing threat landscape are likely to be computationally expensive.

Machine Learning

While statistics, in a traditional sense, is concerned with inference and relies on a set of assumptions about the data, Machine Learning (ML) assumes little, learns from data without being explicitly programmed, and emphasizes prediction over directly modeling the data. ML empirically discovers relationships in the data, focuses on important features and ignores noisy ones, and only has to extract features from the data that are useful in making predictions.

By treating the data generation process as a black box and focusing solely on predictive capability, the primary benefit of ML is its ability to obtain results without explicit assumptions about the data. In particular, when dealing with high-dimensional data, the information contained within them can be encoded within an algorithmic model without having to understand each feature individually. Since discerning the structure within data is not the focus, computer scientists value algorithms that have good scalability and efficiency.

For example, when analyzing disposition of security incident cases by the analyst, ML classifier can be built to model the analyst’s choices. This classifier can then be used to predict the likely outcome of future cases, augmenting analyst’s ability to review cases, thereby shortening triage time and allowing analysts to prioritize their work better. The analyst’s thought process is too complex to model directly, but by focusing only on the quality of predictions, the classifier can avoid this difficulty and reproduce analyst’s choices reasonably well.

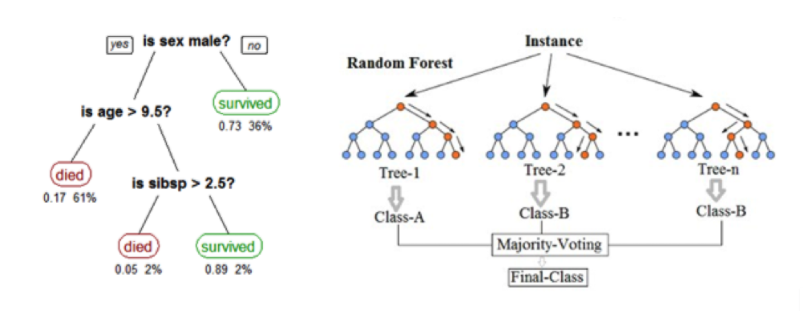
Example of a single Decision Tree (left) and Random Forest ensemble (right).

The Decision Tree is a simple and intuitive algorithm that produces easy to interpret results, but it is not able to capture sophisticated relationships in complex data like this and therefore will have a weak predictive performance. Random Forest, which is an ensemble of decision trees, is a powerful classification and regression algorithm that is generally resistant to overfitting (modeling noise) and has a strong predictive power. Not only can it manage the complexity of the analyst’s decision process, but it can even capture diverse decision paths of different analysts working on the cases.

This power and flexibility comes at a cost: by utilizing essentially a black box approach to prediction, we sacrifice the interpretability of results. Additional statistical facilities are necessary to create such an interpretation. DARPA’s challenge “Explainable Artificial Intelligence” (https://www.darpa.mil/attachments/DARPA-BAA-16-53.pdf) clearly states the need for explainable ML models and the difficulty in developing effective explanation techniques.

Our Approach

At the core of our data science methodology is statistical machine learning, a powerful blend of applied statistics and large-scale machine learning techniques aimed at discovering complex patterns in data and predicting future outcomes. The choice of specific methods within statistical machine learning is governed by the type of data and the problem being solved, with the focus on automated analytics with minimal human intervention. Applied to security analytics, this approach allows us to detect advanced and sophisticated cyber threats in the least amount of time and with the fewest mistakes.